houmies - Quantenchromodynamik

Die Quantenchromodynamik (QCD) ist die quantenfeldtheoretische Beschreibung der starken Wechselwirkung, also im Wesentlichen der Wechselwirkung, welche die Bausteine der Atomkerne zusammenhält.>

Einleitung

Konzeptionell ist die QCD an die Quantenelektrodynamik (QED) angelehnt, die als Eichtheorie mit der abelschen Eichgruppe U(1) die Wechselwirkung elektrisch geladener Teilchen (z. B. Elektron oder Positron) mit Photonen beschreibt. Dabei sind die Photonen selbst ungeladen.

Im Gegensatz dazu ist die Eichgruppe der QCD, SU(3), nicht-abelsch. Die Wechselwirkungsteilchen sind die Gluonen. An die Stelle der elektrischen Ladung als Erhaltungsgröße tritt die Farbladung (daher kommt der Name, Chromodynamik).

Analog zur QED, die nur die Wechselwirkung elektrisch geladener Teilchen betrifft, behandelt die QCD nur Teilchen mit „Farbladung“, die sogenannten Quarks. Quarks können drei verschiede Farbladungen haben, die als rot, grün und blau bezeichnet werden. Diese Benennung ist lediglich eine bequeme Konvention, eine Art "label"; eine Farbe im umgangssprachlichen Sinn besitzen Quarks nicht. Im Unterschied zum elektrisch neutralen Photon in der QED tragen jedoch die Gluonen selbst Farbladung und wechselwirken daher auch miteinander. Die Farbladung der Gluonen besteht aus einer Farbe und einer Anti-Farbe, so dass Gluonenaustausch meist zu „Farbänderungen“ der beteiligten Quarks führt. Die Wechselwirkung der Gluonen bewirkt, dass die Anziehungskraft zwischen den Quarks bei großen Entfernungen zunimmt, ähnlich wie bei einer gespannten sehr steifen Feder oder einem Gummifaden. Wird eine bestimmte „Spannung“ überschritten, reißt der Faden – in der QCD wird in dieser Analogie bei Überschreitung eines gewissen Abstands die Feldenergie so hoch, dass sie in die Bildung neuer Mesonen umgesetzt wird. Daher treten Quarks niemals einzeln auf, sondern nur in gebundenen Zuständen, den Hadronen (Confinement). Das Proton und das Neutron - auch Nukleonen genannt, da aus ihnen die Atomkerne bestehen - sowie die Pionen sind Beispiele für Hadronen.

Da Quarks sowohl eine elektrische als auch eine Farbladung besitzen, wechselwirken sie sowohl elektromagnetisch als auch stark. Da die elektromagnetische Wechselwirkung aber deutlich schwächer ist als die starke Wechselwirkung, kann man ihren Einfluss bei der Wechselwirkung von Quarks in der Regel vernachlässigen und sich daher nur auf den Einfluss der Farbladung beschränken.

Die Quantenchromodynamik ist ein wesentlicher Bestandteil des Standardmodells der Elementarteilchenphysik.

Nichtabelsche Eichgruppe

Die der QCD zugrundeliegende Eichgruppe $SU(3)$ ist nicht-abelsch, das heißt die Multiplikation von zwei Gruppenelementen ist im Allgemeinen nicht kommutativ. Das führt dazu, dass in der Lagrange-Dichte Terme auftreten, die eine Wechselwirkung der Gluonen miteinander bewirken. Aus demselben Grund tragen die Gluonen Farbladung. Diese Selbstwechselwirkung führt dazu, dass die renormierte Kopplungskonstante der QCD sich qualitativ genau entgegengesetzt zur Kopplungskonstante der QED verhält: Sie nimmt für hohe Energien ab. Dies führt bei hohen Energien zu dem Phänomenen der asymptotischen Freiheit und bei niedrige Energien zum Confinement.

Asymptotische Freiheit bedeutet, dass die Quarks sich bei hohen Energien (kleine typische Abstände) wie freie Teilchen verhalten, was konträr zum Verhalten sonstiger Systeme ist, wo schwache Wechselwirkung mit großen Abständen verbunden ist.Confinement bedeutet, dass unterhalb einer Grenzenergie die Kopplungskonstante so groß wird, dass Quarks nur noch in Hadronen auftreten. Da die Kopplungskonstante $α s$ der QCD bei niedrigen Energien kein kleiner Parameter ist, kann die Störungstheorie, mit der sich viele Probleme der QED lösen lassen, nicht angewendet werden. Ein Ansatz zur Lösung der QCD-Gleichungen bei niedrigen Energien sind dagegen Computersimulationen von Gittereichtheorien.

Ein weiterer Ansatz zur quantenfeldtheoretischen Behandlung von Hadronen ist die Verwendung von effektiven Theorien, die für große Energien in die QCD übergehen und für kleine Energien neue Felder mit neuen „effektiven“ Wechselwirkungen einführen. Je nach den zu beschreibenden Hadronen verwendet man verschiedene effektive Theorien. Die chirale Störungstheorie (chiral perturbation theory, CPT) wird für Hadronen verwendet, die nur aus leichten Quarks, also Up-, Down- und Strange-Quarks, aufgebaut sind, die nach der CPT über Mesonen miteinander wechselwirken. Für Hadronen mit genau einem schweren Quark, also einem Charm- oder Bottom-Quark, und sonst nur leichten Quarks wird die effektive Theorie schwerer Quarks (heavy quark effective theory, HQET) verwendet, in welcher das schwere Quark als unendlich schwer angenommen wird, ähnlich der Behandlung des Protons im Wasserstoffatom. Für Hadronen aus zwei schweren Quarks (gebundene Zustände im Quarkonium) wird die sogenannte nichtrelativistische Quantenchromodynamik (nonrelativistic quantum chromodynamics, NRQCD) verwendet.

Abgrenzung zur Kernphysik

Die Stärke der Wechselwirkung führt dazu, dass Protonen und Neutronen im Atomkern viel stärker aneinander gebunden sind als etwa die Elektronen an den Atomkern. Die Beschreibung der Nukleonen ist jedoch ein offenes Problem. Die Quarks besitzen nur 5 % der Masse der Nukleonen, die restlichen 95 % der Nukleonenmasse entstammen der Bindungsenergie der starken Wechselwirkung und der Bewegungsenergie der Quarks. Die Protonen und Neutronen selbst sind farblos und ihre Wechselwirkung wird statt durch die Quantenchromodynamik meist durch eine effektive Theorie beschrieben. Die anziehende Kraft zwischen ihnen beruht nach dieser Theorie auf dem Austausch von Mesonen, insbesondere der leichten Pionen. Die Beschreibung des Verhaltens der Nukleonen über Mesonenaustausch im Atomkern und in Streuexperimenten ist Gegenstand der Kernphysik.

Die starke Wechselwirkung zwischen den Nukleonen im Atomkern ist also viel wirksamer als ihre elektromagnetische Wechselwirkung. Dennoch ergibt die elektrostatische Abstoßung der Protonen ein wichtiges Stabilitätskriterium für Atomkerne. Die starke Wechselwirkung zwischen den Nukleonen wird nämlich, im Gegensatz zur Wechselwirkung zwischen den Quarks, mit zunehmender Entfernung der Nukleonen exponentiell kleiner. Dies liegt an der Tatsache, dass die beteiligten Austauschteilchen im Pion-Austauschmodell eine Masse ungleich Null besitzen. Daher liegt die Reichweite $r c$ der Wechselwirkung zwischen den Nukleonen bei $r_c=frac{hbar}{m_{pi}cdot c}cong 10^{-13}$ cm, also in der Größenordnung der Compton-Wellenlänge der $π$ -Mesonen ( $m π$ ist die Masse des Pions).

Während die Kernkräfte exponentiell mit dem Abstand kleiner werden,

$phi_K(r)proptofrac{1}{r}cdotexpleft(-frac{r}{r_c}right)$ (Yukawa-Potential),

fällt die elektromagnetische Wechselwirkung nur nach dem Potenzgesetz ab

$phi_{EM}(r)proptofrac{1}{r}$ (Coulomb-Potential),

da deren Austauschteilchen, die Photonen, keine Masse besitzen und die Wechselwirkung damit eine unendliche Reichweite hat.

Die starke Wechselwirkung ist also im Wesentlichen auf Abstände der Hadronen, wie sie z. B. im Atomkern auftreten, beschränkt.

Lagrangedichte der QCD

Die QCD ist eine relativistische Quantenfeldtheorie mit der eichinvarianten Lagrangefunktion

$begin{align} mathcal{L}_mathrm{QCD}(q, A) & = bar{q}left(i gamma^mu D_mu - m right) q - frac{1}{4}F^a_{mu nu} F^{mu nu}_a & = bar{q} (i gamma^mu partial_mu - m) q + g bar{q} gamma^mu T_a q A^a_mu - frac{1}{4}F^a_{mu nu} F^{mu nu}_a end{align}$

Aus $bar{q}left(i gamma^mu partial_mu - m right) q$ erhält man durch Anwendung der Euler-Lagrange-Gleichung auf diesen Teil von $mathcal{L}$ die bekannte Dirac-Gleichung und damit

den Propagator für Quarks

Der Term $g bar{q} gamma^mu T_a q A^a_mu$ beschreibt

die Wechselwirkungs-Vertices zwischen Quarks und Gluonen (q-A-Wechselwirkung)

Aus dem Term mit $F^a_{mu nu} F^{mu nu}_a$ erhält man nicht nur

die Propagatoren für Gluonfelder, sondern auch
die 3-Gluon-Gluon-Wechselwirkungs-Vertices
und die 4-Gluon-Gluon-Wechselwirkungs-Vertices

Diese Selbstwechselwirkungsterme der Gluonen, eine Folge der nicht-kommutierenden Generatoren bei nichtabelschen Eichgruppen, stellen den eigentlichen Unterschied zur Lagrangedichte der QED dar.

Aus den einzelnen Termen der Lagrangedichte folgen so die Regeln für Feynmandiagramme in der störungstheoretischen QCD. Es muss allerdings für konkrete Berechnungen noch eine Eichfixierung durchgeführt werden.

Im Einzelnen treten oben folgende Größen auf:

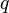$q ,$ , das Quarkfeld (und $bar q = q^dagger gamma^0$ das adjungierte Quarkfeld im Sinne der Dirac´schen relativistischen Quantenmechanik) mit Masse m

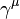$gamma^mu ,$ , die Dirac-Matrizen mit

μ

= 0 bis 3

$A^a_mu ,$ , die acht Eichbosonenfelder (Gluonfelder, a =1 bis 8, entsprechend durch die Gluonen bewirkten Farbänderungen)

$D_mu=partial_mu - igT_aA^a_mu ,$ , die kovariante Ableitung

$,g$ , die Quark-Gluon Kopplungskonstante

$T_a ,$ , ein Erzeugender der Eichgruppe SU(3) (a = 1 bis 8 ), mit den Strukturkonstanten $f_{abc} ,$ (siehe Artikel Gell-Mann-Matrizen)

$F^a_{mu nu} = partial_mu A^a_{nu} - partial_nu A^a_mu + g f^{abc} A^b_mu A^c_nu ,$ , der Feldstärketensor des Eichbosonenfeldes.

Wegen "Div Rot = 0" gibt die Summe der ersten beiden Terme auf der rechten Seite des Feldstärketensors bei Divergenzbildung immer Null, im Unterschied zum nicht-abelschen Anteil, ~ g.

(Das Hinauf- und Hinabziehen zwischen unteren und oberen Indizes geschieht bezüglich a immer mit der trivialen Signatur, +, so dass also für die Strukturkonstanten $f_{abc}equiv f^a_{bc}$ gilt. Bezüglich der μ und ν erfolgt es dagegen mit der relativistischen Signatur, (+−−−).)

Quark-Antiquark-Potential

Aus dem Vergleich von Energieniveauschemas z. B. von Positronium und Charmonium lässt sich mithilfe dieser Lagrangefunktion zeigen, dass sich die starke Wechselwirkung und die elektromagnetische Wechselwirkung nicht nur quantitativ unterscheiden: Zwar verhält sich das Quark-Antiquark-Potential bei kleinen Abständen ähnlich wie bei der elektromagnetischen WW (der Term ~ α entspricht der Coulomb-Anziehung entgegengesetzter Farbladungen). Bei größeren Abständen ergibt sich dagegen wegen der oben erwähnten Feder-Analogie ein wesentlich anderes Verhalten, das von den Gluonen verursacht wird und auf "Confinement" hinausläuft. Es entspricht der Elastizität eines verstreckten Polymers (Gummielastizität).

Insgesamt ist die effektive potentielle Energie:

$V(r)=-frac{4}{3}frac{alpha_s(r)hbar c}{r}+kcdot r,,$

mit der vom Impulsübertrag Q² (und damit vom Abstand r) abhängigen starken Kopplungs-„konstanten“ („gleitende Kopplung“) $α s$ . Für sie gilt in erster Ordnung der Störungstheorie

$alpha_s(Q^2) = frac{12cdotpi}{(33-2n_f)cdot ln(Q^2/Lambda^2)},,$

mit der (auch von Q² abhängigen) Anzahl der beteiligten Quarkfamilien $n_f,.$

Der linear mit dem Radius zunehmende Term beschreibt das Confinement-Verhalten, während der erste Term eine Coulomb-Form besitzt und für sehr hohen Energien, bei denen $alpha_s ll 1$ klein ist, Rechnungen in Störungstheorie erlaubt. Mit n_f fließt hier in das Verhalten auch die Anzahl der Familien (Flavor-Freiheitsgrade) des Standardmodells der Elementarteilchenphysik ein.

Der charakteristische Radius, $R_c=sqrt{frac{4hbar calpha_s/3}{k}},,$ bei dem das Verhalten von V(r) „umschlägt“ (bei diesem Radius ist das Potential gleich Null), kann mit dem Radius der vormaligen Bag-Modelle der Hadronen in Beziehung gebracht werden;(Größenordnung von R_c: 1 fm (=10^-15 m)).

Gittereichtheorie

→ Hauptartikel: Gittereichtheorie

Computersimulationen der Quantenchromodynamik führt man heutzutage meist im Rahmen der sog. Gittereichtheorien durch (in der englischsprachigen Literatur spricht man auch von der sog. „Gitter-QCD“). Inzwischen gibt es viele über „Szenarien“ weit hinausgehende Resultate dieser Theorien im für die QCD relevanten Fall. Diese Arbeiten benötigen die ursprünglich in festkörpertheoretischem Zusammenhang aufgestellten Modelle Franz Wegners in der Regel nicht mehr. Zumal diese seinerzeit aus verschiedenen Gründen in der statistischen Physik nur unter Spezialisten Beachtung fanden. Diese Beachtung war aber vor allem wegen der Eichinvarianz und der damit verbundenen lokalen Besonderheiten für die thermodynamischen Korrelationsfunktionen beträchtlich. Bis dahin standen mehr die globalen Zusammenhänge im Vordergrund. Trotzdem ist die Gittereichtheorie selbst in der Hochenergiephysik nicht auf die Quantenchromodynamik beschränkt

Die amerikanischen Wissenschaftler Kenneth Wilson und John Kogut haben in mehreren Arbeiten die Gittereichtheorie der QCD zur numerisch effektiven Methode gemacht. Der wesentliche Ansatz ihrer Veröffentlichungen ist, dass

aus den drei Raumdimensionen und der Zeitdimension der relativistischen Quantenfeldtheorie vier in klassischer statistischer Mechanik zu behandelnde euklidische Dimensionen gewonnen werden (3+1 relativistisch → 4 euklidisch), wobei
zur numerischen Realisierung des euklidischen Gittermodells das Wirkungsfunktional der QCD so diskretisiert wird, dass eine möglichst effektive und zugleich die wichtige chirale Symmetrie möglichst perfekt realisierende Theorie entsteht.

Der Name Wilson hat auch durch eine als Wilson-Loop bezeichnete Schleifenvariable zur Diskretisierung der Feldenergie – das ist der letzte Term der obigen Lagrangedichte – Eingang in das Sachverzeichnis der Theorie gefunden. Diese Variable dient darüber hinaus zur Kennzeichnung des Confinement.

Forscher und Nobelpreise

Einer der Begründer der Quantenchromodynamik (und davor des Quarkmodells) Murray Gell-Mann erhielt für seine schon damals (vor Einführung der QCD) zahlreichen Beiträge zur Theorie der starken Wechselwirkung bereits 1969 den Nobelpreis der Physik. Bei seinen Pionierarbeiten zur QCD arbeitete er mit Harald Fritzsch und Heinrich Leutwyler zusammen.

Am 5. Oktober 2004 wurden David Gross, David Politzer und Frank Wilczek für ihre Arbeiten zur Quantenchromodynamik der „starken Wechselwirkung“ mit dem Nobelpreis für Physik ausgezeichnet. Sie entdeckten Anfang der 1970er Jahre, dass die starke Wechselwirkung der Quarks schwächer wird, je näher sie sich sind. In direkter Nähe verhalten sich Quarks gewissermaßen wie freie Partikel, was die Ergebnisse der damaligen tiefinelastischen Streuexperimente theoretisch begründete.

Quelle: http://de.wikipedia.org/wiki/Quantenchromodynamik